快速排序

快速排序是最常用的排序算法了。它的复杂度为 O(nlog^n)，且它的性能通常比其他的复杂度为 O(nlog^n) 的排序算法要好。

另外，通常在面试中有极大的可能性，面试官会让你手写写一个快速排序算法。

所以学会快速排序对实际工作或是面试都是很重要的，现在就开始吧~

实现

首先定义一个快速排序函数：

1
2
3
function quickSort(arr) {
  //code
}

现在开始完成 quickSort 的核心功能，快速排序是基于递归算法实现的。因此我们需要添加结束条件：

1
2
3
function quickSort(arr) {
    if (arr.length < 2) return arr
}

这意味着如果传入的数组长度小于2，直接返回即可。因为我们不需要对一个空数组或只有一个元素的数组进行排序。

下一步，定义三个重要的变量：

  • pivot - 主要用于在数组中选择一个与其他元素进行比较的元素(在本例子中用的是数组第一个元素)

  • left - 小于pivot的元素存放的数组

  • right - 大于pivot的元素存放的数组

1
2
3
4
5
6
function quickSort(arr) {
  if (arr.length < 2) return arr;
  let pivot = arr[0];
  const left = [];
  const right = [];
}

现在我们需要在左和右传递数组的元素数组。这需要一个 for 循环。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
function quickSort(arr) {
  if (arr.length < 2) return arr;
  let pivot = arr[0];
  const left = [];
  const right = [];
    
  for (let i = 1; i < arr.length; i++) {
    if (pivot > arr[i]) {
      left.push(arr[i]);
    } else {
      right.push(arr[i]);
    }
  }
}

这里我们遍历数组的每个元素和 pivot 比较，小于 pivot 加入 left 数组，否则加入 right 数组。

假设我们传入的是如下的数组：**[5, 2, 6, 1, 30, -10]**

pivot 取数组的第一个元素：5。首先5和2比较。2小于5(2 < 5),因此2添加到 left 数组；然后比较5和6，6大于5(6 > 5)，然后把6加到 right 数组。

最后 left 和 right 分别为：

  • left: [2, 1, -10]
  • right: [6, 30]

现在你可能有一个问题: “如何实现数组排序?“ 答案很简单。我们需要递归调用快速排序数组以及在它们之间插入 pivot 。为什么？因为 pivot 位于 left 数组元素和 right 数组的元素。

最终, 让我们回到代码。返回最终排序后的数组:

1
return quickSort(left).concat(pivot, quickSort(right));

为了帮助理解快速排序算法，还是以 [5, 2, 6, 1, 30, -10] 为例，详细解释一下排序的过程：

第一次迭代后的结果为：

  • left: [2, 1, -10]
  • right: [6, 30]

分别对 left 和 right 进行递归调用，意味着 2 作为 pivot 分别与 1, -10 进行比较，整个快速排序的执行过程：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
arr: [5, 2, 6, 1, 30, -10]      pivot: 5
│
└───left: [2, 1, -10]           pivot: 2
│   │
│   └───left: [1, -10]          pivot: 1
│   │   │
│   │   └───left: [-10]
│   │   │
│   │   └───right: []
│   │
│   └───right: []
│
└───right: [6, 30]              pivot：6
│   │
│   └───left: []
│   │
│   └───right: [30]

最终，将每个划分后的数组通过 concat() 连接起来就是最终排好序的最终数组。

1
return quickSort(left).concat(pivot, quickSort(right));

完整的代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
function quickSort(arr) {
  if (arr.length < 2) return arr;
  let pivot = arr[0];
  const left = [];
  const right = [];
    
  for (let i = 1; i < arr.length; i++) {
    if (pivot > arr[i]) {
      left.push(arr[i]);
    } else {
      right.push(arr[i]);
    }
  }
  return quickSort(left).concat(pivot, quickSort(right));
}

执行效率

快速排序算法的时间复杂度是O(nlogn), n 是一个数组的长度。最坏的情况下是O(n²)。

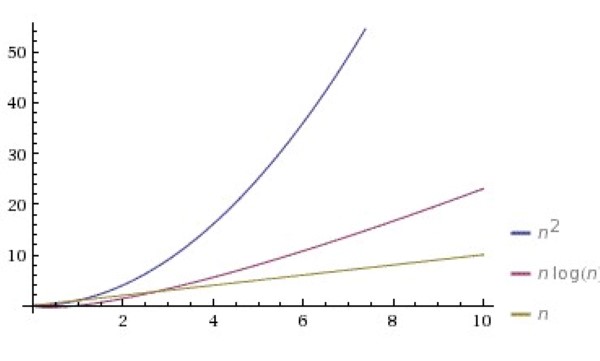
efficiency

为了达到平均的情况下，我们需要随即选择一个数组项作为主元(pivot)。我通常这样做: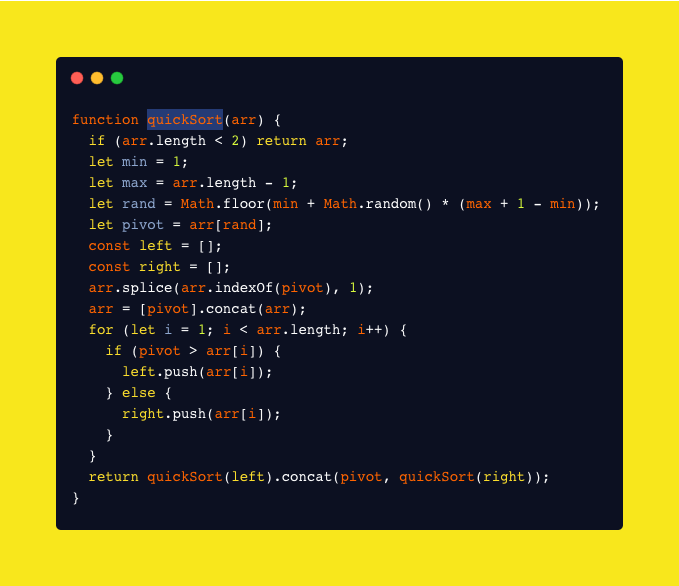
quickSort2

总结

我相信在阅读这篇文章之后你已经完全理解快速排序算法，面试的时候也会更有信心。

如果你有更简单的解释JS的快速排序算法。请通过评论告诉我!